解离能计算工作流和原理

1 思维导图

2 初始Image设置

2.1 初始结构准备

可以先进行分子动力学来进行预优化！

2.1.1 读取Slab

可以在VESTA中设定晶格常数（空间群）和原子位置，导出为合适的格式即可。用

slab = read('XXX.cif')`

2.1.2 吸附原子优化

from ase import Atoms
from ase.optimize import BFGS
from gpaw import GPAW
Mg2S2 = Atoms('Mg2S2',[[0,0,0],[3.7,0,0],[1.85,1.85,0],[1.85,-1.85,0]])
Mg2S2.center(vacuum=3.0) # x,y,z方向各加3 A的真空层
Mg2S2.calc = GPAW(mode='lcao', basis='dzp', txt='gpaw.txt')
opt = BFGS(atoms, trajectory='Mg2S2.traj')
opt.run(fmax=0.05)

2.1.3 将Mg2S2附加到slab上

add_adsorbate(slab,Mg2S2,height=4.0,position=(2.383, 5.455))

2.2 初始结构优化 ¹²

显然，晶格常数cell和原子位置postion都会对能量造成影响，晶格常数实际上固定了位于格点的原子间距。可以全部采用实验值或者部分采用实验值进行优化。对于吸附体系显然没有实验值，所以需要一起优化。使用

ucf = UnitCellFilter(slab)
qn = QuasiNewton(ucf)

或者

ecf = ExpCellFilter(atoms)
qn = QuasiNewton(ecf)

但是，一起优化可能耗时长，可以用set_constraints的FixAtoms命令固定某些原子。准牛顿算法进行几何优化。用ase.constraints.StrainFilter固定某些方向。

前期的粗略计算可以先固定碳原子和晶格常数，后期再考虑影响大不大。

print(slab.constraint)
c = FixAtoms(mask=[atom.symbol == 'C' for atom in atoms])
slab.set_constraint(c)

2.3 超参数设置³

初始优化尽量快速，Ecut采用默认340 eV，泛函采用PBE，优化算法用QuasiNewton == BFGSLineSearch。

默认的k点为gamma点，即kpts=(1,1,1)，多取几个点计算时间就会多几倍（可以并行），总能量是多个k点能量的平均，如果k点取得越密，该平均值越能反应布里渊区的电子能量分布。由于z方向不具备周期性，所以z方向的k点设置为0。不同k值反映了不同方向传播的电子，由于感受的周期不同，所以具有不同的能量。

后期可以进行修改超参数Ecut、Kpts、Ediff等或者扩胞。

由于我们关心的是相对能量而非决定能量，所以不用太关心超参数优化到最好的值。

3 最终Image设置

按照上述步骤建立final_image(如何选择初始的位置？)

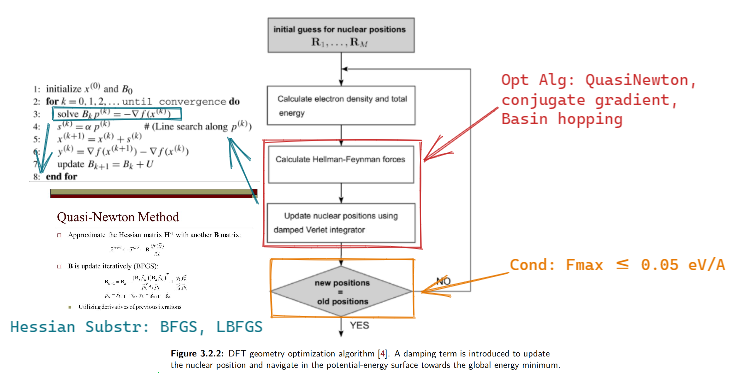
4 优化算法

建立中间图像


configs = [initial.copy() for i in range(8)] + [final] # 8 of initial and 1 of final images

添加计算器


for config in configs:

    config.calc = GPAW() # config the calculator of every image, only the internal images (not the endpoints) need have calculators attached.

线性插值并用CI-NEB算法


band = NEB(configs)

band.interpolate() # linear interpolation

relax = QuasiNewton(band, trajectory='XXX.traj')

绘制图像


import matplotlib.pyplot as plt

e0 = initial.get_potential_energy() 

E = [config.get_potential_energy() - e0 for config in configs]

plt.plot(E)

5 并行计算、io、时间估计、可视化

结构优化时间 = 单次SCF的时间 × N，N取决于算法的高效性。因为下一次SCF取决于上一次SCF的结果，所以无法有效进行并行计算。
CI-NEB时间 = 结构优化时间 x Image数量。每个Image可以各自进行结构优化，所以可以并行。

!mpiexec -np 4 python3 xxx.py

write('xxx.traj', slab)
write('xxx.cif', slab)
!ase -gui xxx.traj/cif

将cif文件拖入http://www.openmx-square.org/viewer/

6 问题

具体的能量值代表什么？如何考虑费米狄拉克分布width=0.1000 eV？
实空间间隔如何取的？具体的能带数量如何通过Ecut求出？