变换原则
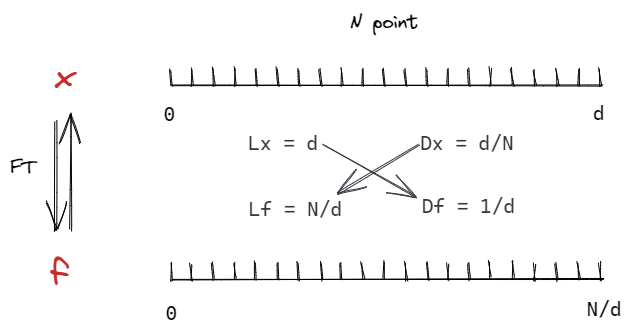
在不丢失信息的情况下:
实空间越长(d越大),频率空间越密。所以超胞越大,对应的频率空间点密度越大
实空间越密(N越大),频率空间越长,倒格矢G越大。所以实空间走得越精细,频率空间需要的截止能量Ecut就越大。避免基函数的数量比价电子的数量还少。
本质上是对易关系:
$$
\Delta x \Delta f = 1
$$
傅里叶变换
引言
要对一个非周期且连续的函数做傅里叶变换,可以分为两步走。
- 对这个连续函数进行
抽样。变成离散的函数,为了最后能恢复出原信号,抽样频率要满足抽样定理。
## 抽样
t = np.linspace(0,1,Fs)
y = np.sin(2*np.pi*f1*t)*np.exp(-t/tao)
- 将这个离散函数
周期化。然后求出其傅里叶级数,即DFT,此时求得的傅里叶级数是离散非周期傅里叶变换的抽样,这个抽样同样要满足抽样定理,也就是扩展的周期要足够大。 在具体实现的时候,并不用做周期化,因为我们调用FFT实现的就是DFT。FFT跟DFT区别只不过FFT利用傅里叶级数的特点降低了算法的时间复杂度,没有信息的丢失。
完整代码
import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
Fs = 1024
tao = 1/4
f1 = 200
t = np.linspace(0,1,Fs) # 如果区间从(0,2),那么FFT出来频率的结果就不对。因为频率间隔不是1,而是1/2了
y = np.sin(2*np.pi*f1*t)*np.exp(-t/tao)
plt.subplot(121)
plt.plot(t,y)
plt.title('initial wave')
Y = np.abs(fft(y))/Fs
half_Y = Y[range(int(Fs/2))]
plt.subplot(122)
plt.plot(half_Y)
plt.title('FFT')